1 Background

1-1 Advantages of Transformer architecture

Compared to other sequence-modeling models:

parallelizable
less time to train

1-2 Basic Structures of Transformer (Encoder,Decoder)

Encoder:

A stack of basic blocks (\(N=6\))
A basic Encode-block mainly consists of two types of sublayers:
- Multi-Head Self-Attention (MHSA)
- Position-wise fully connected feed-forward layer (FF)
- Other core components
  - residual connection
  - layer normalization

Decoder:

Also a stack of basic blocks (\(N=6\))
A basic Decoder-block mainly consists of three types of sublayers:
- Masked Multi-Head Self-Attention
- Encoder-Decoder Multi-Head Attention (MHA)
- Fully connected feed-forward layer
- Other core components
  - residual connection
  - layer normalization

2- Build a Transformer model with PyTorch from scratch

2-1 Import Necessary Libraries

import torch.nn as nn
import torch
import torch.nn.functional as F
import math

2-2 Basic Components

2-2-1 Word Embeddings

A word embedding layer is to convert a input sequence with \(shape=(B, L)\) into a sequence of word embeddings with \(shape=(B, L, D)\), where

\(B\) is the batch size
\(L\) is the length of the sequence
\(D\) is the dimension of embedding

A embedding layer can be easily implemented by PyTorch:

embeddin_layer = nn.Embedding(vocab_size, embed_dim)

2-2-2 Positional Encoding

In the original paper, the positional encoding was created under the sinusoid form.

\[PE(pos, 2i) = \sin(\frac{pos}{10000^{2i/D}})\] \[PE(pos, 2i+1) = \cos(\frac{pos}{10000^{2i/D}})\]

where

\(pos\) refer to the position in the setence (along the length dimension)
\(i\) refers to the position along the embedding vector dimension

We can implement the positional encoder as the following class

class PositionalEncoder(nn.Module):
    def __init__(self, max_seq_len, embed_dim=512) -> None:
        super(PositionalEncoder, self).__init__()
        self.embed_dim = embed_dim
        self.max_seq_len = max_seq_len

        self.pos_enc = nn.Parameter(
            torch.zeros(1, max_seq_len, embed_dim), requires_grad=False
        )  # L * D

        ### Method 1: for-loop
        # for pos in range(max_seq_len):
        #     for i in range(0, embed_dim, 2):
        #         self.pos_enc.data[0, pos, i] = math.sin(
        #             pos / math.pow(10000, i / embed_dim)
        #         )
        #         self.pos_enc.data[0, pos, i + 1] = math.cos(
        #             pos / math.pow(10000, i / embed_dim)
        #         )

        # Method 2: meshgrid
        rowv, colv = torch.meshgrid(
            torch.arange(max_seq_len), torch.arange(0, embed_dim, 2), indexing="ij"
        )
        self.pos_enc.data[0, rowv, colv] = torch.from_numpy(
            np.sin(rowv / np.power(10000, colv / embed_dim))
        )
        self.pos_enc.data[0, rowv, colv + 1] = torch.from_numpy(
            np.cos(rowv / np.power(10000, colv / embed_dim))
        )

    def forward(self, x):
        seq_len = x.shape[1]
        x += self.pos_enc[:, :seq_len, :]
        return x

2-2-3 Multi-Head Attention (MHA) Block

2-2-3-1 FeedForward layer

According to the original paper, this layer is a two-layer fully connected layer.

class FeedForwardLayer(nn.Module):
    def __init__(self, embed_dim=512, hidden_dim=2048):
        super(FeedForwardLayer, self).__init__()
        self.fc1 = nn.Linear(embed_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, embed_dim)

    def forward(self, x):
        out = self.fc2(F.relu(self.fc1(x)))
        return out

2-2-3-2 Multi-Head Attention

Now, let’s move to the most core component of Transformer model, Multi-Head Attention mechanism.

class MultiHeadAttention(nn.Module):
    def __init__(self, embed_dim=512, n_heads=8):
        super(MultiHeadAttention, self).__init__()
        assert (embed_dim % n_heads) == 0
        self.embed_dim = embed_dim
        self.n_heads = n_heads
        self.single_head_dim = embed_dim // n_heads

        self.q_proj = nn.Linear(embed_dim, embed_dim)
        self.k_proj = nn.Linear(embed_dim, embed_dim)
        self.v_proj = nn.Linear(embed_dim, embed_dim)
        self.final_projector = nn.Linear(embed_dim, embed_dim)

    def forward(self, x_q, x_k, x_v, mask=False):
        B, L = x_q.shape[0], x_q.shape[1]
        ### x_q, x_k, x_v: shape=(B, L, D)
        queries = self.q_proj(x_q)
        keys = self.k_proj(x_k)
        values = self.q_proj(x_v)

        queries = queries.view(B, L, self.n_heads, self.single_head_dim)  # (B,L,h,D/h)
        keys = keys.view(B, L, self.n_heads, self.single_head_dim)  # (B,L,h,D/h)
        values = values.view(B, L, self.n_heads, self.single_head_dim)  # (B,L,h,D/h)

        queries = queries.transpose(1, 2)  # (B,h,L,D/h)
        keys = keys.transpose(1, 2)  # (B,h, L, D/h)
        values = values.transpose(1, 2)  # (B,h, L,D/h)

        # Q*K^T (B,h,L,D/h) * (B,h,D/h,L) -> (B,h,L,L)
        logits = torch.softmax(torch.matmul(queries, keys.transpose(-1, -2)), dim=-1)
        if mask:
            m = torch.tril(torch.ones(size=(L, L))).reshape(1, 1, L, L)
            logits *= m
        # (B,h,L,L) * (B,h,L,D/h) -> (B,h,L,D/h)
        attention = torch.matmul(logits / math.sqrt(self.single_head_dim), values)
        # (B,h,L,D/h) -> (B,L,h,D/h) -> (B,L,D)
        attention = attention.transpose(1, 2).reshape(B, L, self.embed_dim)
        out = self.final_projector(attention)
        return out

Remark: The Masked Multi-Head Self-Attention layer in the Decoder needs to prevent leftward information flow. The output embeddings (as the input of the Decoder) are offset to right by one position during training. This is to ensure that the prediction for position p=i can depend only the known outputs at position p<i.

For example, if the target sequence is [I], [am], [fine], <end>, the queries and keys relevant to this sequence are

[I]: \(Q_{1}, K_{1}\)

[am]: \(Q_{2}, K_{2}\)

[fine]: \(Q_{3}, K_{3}\)

<end>: \(Q_{4}, K_{4}\)

Then, the right-shifted sequence is <start>, [I], [am], [fine], <end>. The queries and keys relevant to this sequence are

<start>: \(Q_{1}^{\prime}, K_{1}^{\prime}\)

[I]: \(Q_{2}^{\prime}, K_{2}^{\prime}=Q_{1}, K_{1}\)

[am]: \(Q_{3}^{\prime}, K_{3}^{\prime}=Q_{2}, K_{2}\)

[fine]: \(Q_{4}^{\prime}, K_{4}^{\prime}=Q_{3}, K_{3}\)

<end>: \(Q_{5}^{\prime}, K_{5}^{\prime}=Q_{4}, K_{4}\)

Let’s consider the attention process, especially the \(Q\cdot K^{\top}\) operation. Since the prediction for position p=i should depend only the known outputs at position p<i, the elements above the diagonal of \(Q\cdot K^{\top}\) (e.g., \(Q_{2} \cdot K_{3}^{\top}\)), should be removed before the softmax operation, while the elements on or below the diagonal should be kept (e.g., \(Q_{2} \cdot K_{2}^{\top}\), \(Q_{2} \cdot K_{1}^{\top}\)).

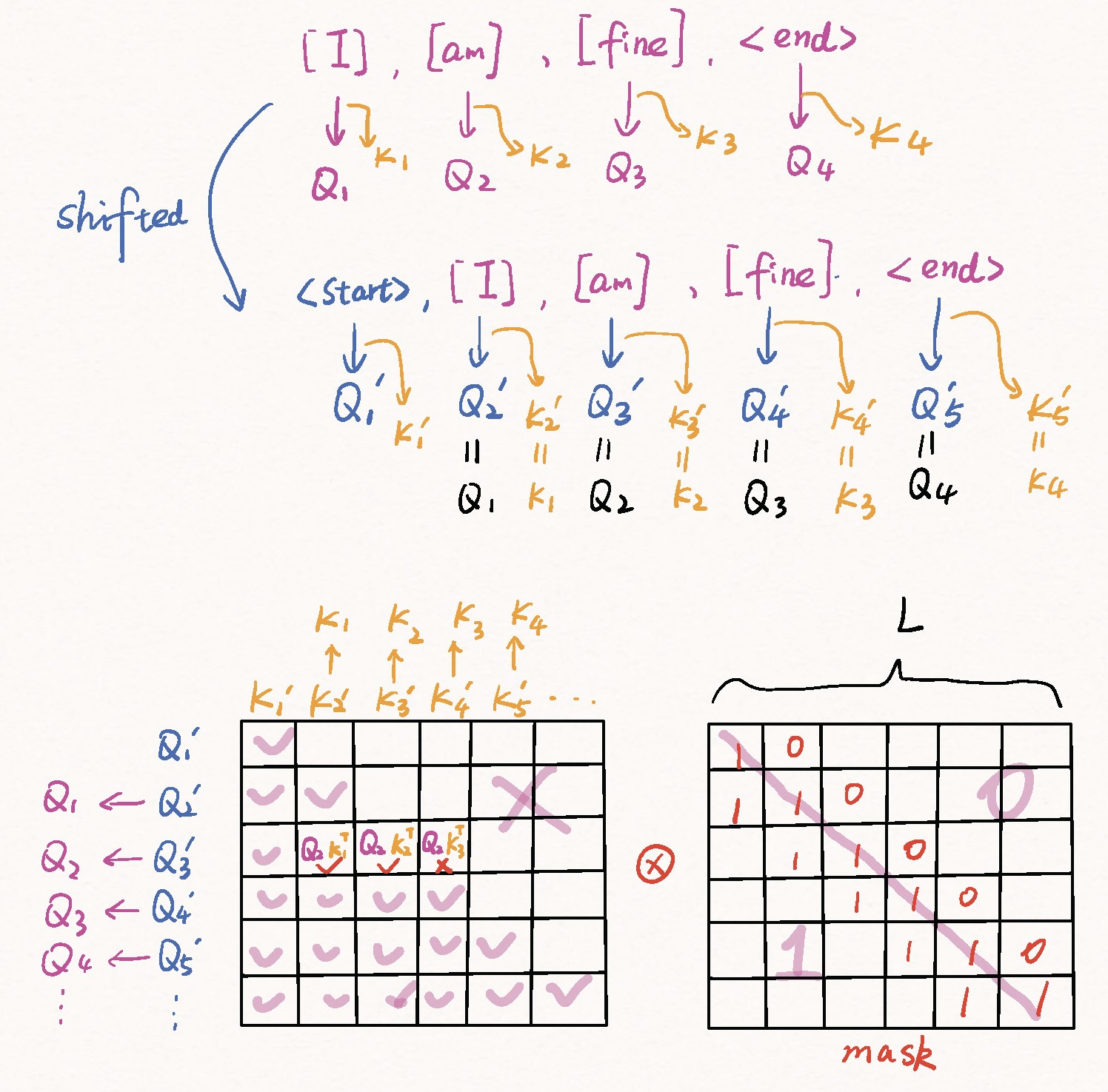
Masked Attention

Thus, the mask matrix should be a lower-triangluar bool matrix with entries 1 (the upper entries should be 0). This mask can be easily obtained with PyTorch:

mask = torch.tril(torch.ones(size=(L, L)))

Remark: here is also an Encoder-Decoder attention mechanism in the Multi-Head Attention layers in the Decoder.

For the MHSA in the Encoder or the masked MHSA in the decoder, the query, key, value are from all from the output of the previous layer.
However, in the Encoder-Decoder MHA module in the decoder block, the queries Q is from the output of the previous decoder layer, but the keys K and the values V are obtained from the Encoder output.

2-2-3-3 A basic Encoder block

class EncoderBlock(nn.Module):
    def __init__(self, embed_dim=512, n_heads=8, ff_hidden_dim=2048):
        super(EncoderBlock, self).__init__()

        self.mhsa = MultiHeadAttention(embed_dim=embed_dim, n_heads=n_heads)
        self.ln1 = nn.LayerNorm(normalized_shape=embed_dim)

        self.ff = FeedForwardLayer(embed_dim=embed_dim, hidden_dim=ff_hidden_dim)
        self.ln2 = nn.LayerNorm(normalized_shape=embed_dim)

    def forward(self, x):
        # x.shape = (B,L,D)
        out = x + self.mhsa(x, x, x, mask=False)
        out = self.ln1(out)

        out = out + self.ff(out)
        out = self.ln2(out)
        return out

2-2-3-4 A basic Decoder block

class DecoderBlock(nn.Module):
    def __init__(self, embed_dim=512, n_heads=8, ff_hidden_dim=2048):
        super(DecoderBlock, self).__init__()

        self.masked_mhsa = MultiHeadAttention(embed_dim=embed_dim, n_heads=n_heads)
        self.ln1 = nn.LayerNorm(normalized_shape=embed_dim)

        self.mha = MultiHeadAttention(embed_dim=embed_dim, n_heads=n_heads)
        self.ln2 = nn.LayerNorm(normalized_shape=embed_dim)

        self.ff = FeedForwardLayer(embed_dim=embed_dim, hidden_dim=ff_hidden_dim)
        self.ln3 = nn.LayerNorm(normalized_shape=embed_dim)

    def forward(self, x, enc_out):
        # x.shape = (B,L,D)
        out = x + self.masked_mhsa(x, x, x, mask=True)
        out = self.ln1(out)

        out = out + self.mha(x, enc_out, enc_out)
        out = self.ln2(out)

        out = out + self.ff(out)
        out = self.ln3(out)
        return out

2-3 Build Encoder and Decoder

2-3-1 Encoder

class TransformerEncoder(nn.Module):
    def __init__(
        self,
        seq_len,
        src_vocab_size,
        embed_dim=512,
        n_heads=8,
        ff_hidden_dim=2048,
        num_layers=6,
    ):
        super(TransformerEncoder, self).__init__()
        self.seq_len = seq_len
        self.src_vocab_size = src_vocab_size
        self.embed_dim = embed_dim
        self.n_heads = n_heads
        self.ff_hidden_dim = ff_hidden_dim
        self.num_layers = num_layers

        self.embedding_layer = nn.Embedding(
            num_embeddings=src_vocab_size, embedding_dim=embed_dim
        )

        self.positional_encoder = PositionalEncoder(
            max_seq_len=seq_len, embed_dim=embed_dim
        )

        self.layers = nn.ModuleList(
            [
                EncoderBlock(
                    embed_dim=embed_dim, n_heads=n_heads, ff_hidden_dim=ff_hidden_dim
                )
                for _ in range(num_layers)
            ]
        )

    def forward(self, x):
        embedding = self.embedding_layer(x)
        out = self.positional_encoder(embedding)
        for layer in self.layers:
            out = layer(out)
        return out

2-3-2 Decoder

The Decoder is a little different. As described before, it also accepts the Encoder output x_enc in the forward() function.

class TransformerDecoder(nn.Module):
    def __init__(
        self,
        seq_len,
        tgt_vocab_size,
        embed_dim=512,
        n_heads=8,
        ff_hidden_dim=2048,
        num_layers=6,
    ):
        super(TransformerDecoder, self).__init__()
        self.seq_len = seq_len
        self.tgt_vocab_size = tgt_vocab_size
        self.embed_dim = embed_dim
        self.n_heads = n_heads
        self.ff_hidden_dim = ff_hidden_dim
        self.num_layers = num_layers

        self.embedding_layer = nn.Embedding(
            num_embeddings=tgt_vocab_size, embedding_dim=embed_dim
        )

        self.positional_encoder = PositionalEncoder(
            max_seq_len=seq_len, embed_dim=embed_dim
        )

        self.layers = nn.ModuleList(
            [
                DecoderBlock(
                    embed_dim=embed_dim, n_heads=n_heads, ff_hidden_dim=ff_hidden_dim
                )
                for _ in range(num_layers)
            ]
        )
        self.fc = nn.Linear(embed_dim, tgt_vocab_size)

    def forward(self, x, enc_out):
        embedding = self.embedding_layer(x)
        out = self.positional_encoder(embedding)
        for layer in self.layers:
            out = layer(out, enc_out)
        out = F.softmax(self.fc(out), dim=-1)
        return out

2-4 Then you get Transformer model

class Transformer(nn.Module):
    def __init__(
        self,
        seq_len,
        src_vocab_size,
        tgt_vocab_size,
        embed_dim=512,
        n_heads=8,
        ff_hidden_dim=2048,
        num_layers=6,
    ):
        super(Transformer, self).__init__()
        self.seq_len = seq_len
        self.src_vocab_size = src_vocab_size
        self.tgt_vocab_size = tgt_vocab_size
        self.embed_dim = embed_dim
        self.n_heads = n_heads
        self.ff_hidden_dim = ff_hidden_dim
        self.num_layers = num_layers

        self.encoder = TransformerEncoder(
            seq_len=seq_len,
            src_vocab_size=src_vocab_size,
            embed_dim=embed_dim,
            n_heads=n_heads,
            ff_hidden_dim=ff_hidden_dim,
            num_layers=num_layers,
        )
        self.decoder = TransformerDecoder(
            seq_len=seq_len,
            tgt_vocab_size=tgt_vocab_size,
            embed_dim=embed_dim,
            n_heads=n_heads,
            ff_hidden_dim=ff_hidden_dim,
            num_layers=num_layers,
        )

    def forward(self, src, tgt):
        enc_out = self.encoder(src)
        out = self.decoder(tgt, enc_out)
        return out

Remark: The Inference Process of Transformer The inference of the Transformer (Decoder) is auto-regressive, which means that the previous predicted (or generated) content will serve as the input during the next-iteration inference.

Transformer model from scratch