LLMs Efficient Inference with KV-cache
KV-cache in Large Language Models and its implementation (GPT-2 model as an example)
1 Background
In recent years, large language models (LLMs), such as GPT, BERT, and their derivatives relying on the Transformer architecture, has become the backbone of state-of-the-art NLP models. A critical component of the Transformer architecture is the attention mechanism, where each token attends to every other token in the input sequence. While this approach enables powerful contextual understanding, it also introduces significant computational challenges, particularly for long sequences and large models with billions of parameters. The language models generate tokens in an auto-regressive manner, and the quadratic complexity of self-attention with respect to sequence length leads to increasing memory and latency requirements, making inference slower and more expensive.
To address these challenges, researchers introduced the concept of key-value (KV) caching. KV-cache optimizes Transformer inference by storing the key and value vectors computed during forward passes and reusing them in subsequent tokens prediction. This caching mechanism guarantees faster text generation with lower memory footprints.
Understanding KV-cache is essential for optimizing large-scale deployments of LLMs, as it forms the foundation for techniques such as streaming inference and efficient model serving. In the following sections, we will delve deeper by answering the following questionsL
- why we need KV-cache;
- how KV-cache works;
- how to implement it in practice (taking GPT-2 model as an example)
2 KV-cache Explanation
Why we can accelerate the inference by caching K (keys) and V (values) in LLMs? Why there is no need to cache Q (queries)?
2-1 Attention Mechanism Recall
Let’s recall the math behind attention mechanism:
\[\text{Attention}(Q, K, V) = \text{softmax}\biggl( \frac{Q\cdot K^\top}{\sqrt{d}} \biggl)\cdot V\]where $Q,K,V \in \mathbb{R}^{L \times d}$. $L$ indicates the sequence length, and $d$ is the embedding dimensionality. To represent the above operations, we can write $Q,K,V$ with row vectors, e.g., $Q=\begin{bmatrix} q_1 \ q_2 \ \cdots \ q_L \end{bmatrix}$, where $q_1, q_2, \cdots, q_L \in \mathbb{R}^{1 \times d}$.
Please note that each row $q_t, k_t, v_t$ represents the related embedding of token-$t$. Thus,
\[Q\cdot K^\top = \begin{bmatrix} q_1\cdot k_1 & q_1 \cdot k_2 & \cdots & q_1 \cdot k_L \\ q_2\cdot k_1 & q_2 \cdot k_2 & \cdots & q_2 \cdot k_L \\ \vdots & \vdots & \ddots & \vdots \\ q_L\cdot k_1 & q_L \cdot k_2 & \cdots & q_L \cdot k_L \\ \end{bmatrix} \in \mathbb{R}^{L\times L}\]Denote
\[\text{attn_score} = \text{softmax}\bigl( \frac{Q\cdot K^\top}{\sqrt{d}} \bigl) =\begin{bmatrix} S_1(q_1\cdot k_1) & S_1(q_1 \cdot k_2) & \cdots & S_1(q_1 \cdot k_L) \\ S_2(q_2\cdot k_1) & S_2(q_2 \cdot k_2) & \cdots & S_2(q_2 \cdot k_L) \\ \vdots & \vdots & \ddots & \vdots \\ S_L(q_L\cdot k_1) & S_L(q_L \cdot k_2) & \cdots & S_L(q_L \cdot k_L) \\ \end{bmatrix}\]With a slight abuse of notation, $S_{t}(q_t\cdot k_i)$ indicates applying the softmatx operator in Line-$t$ to the result $q_t\cdot k_i$.
During the training and inference of the recent Decoder-only LLMs (e.g., GPT-series), each token is predicted based on previous tokens. Then, the causal mask is introduced to make sure the model can only attend to previous tokens, not future ones. The masked attention scores become:
\[\text{masked_attn_score} = \text{softmax}\bigl( \frac{Q\cdot K^\top}{\sqrt{d}} \odot M \bigl) =\begin{bmatrix} S_1(q_1\cdot k_1) & 0 & \cdots & 0 \\ S_2(q_2\cdot k_1) & S_2(q_2 \cdot k_2) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ S_L(q_L\cdot k_1) & S_L(q_L \cdot k_2) & \cdots & S_L(q_L \cdot k_L) \\ \end{bmatrix}\]The output of the attention module is:
\[\text{softmax}\biggl( \frac{Q\cdot K^\top}{\sqrt{d}} \odot M \biggl)\cdot V= \begin{bmatrix} S_1(q_1\cdot k_1)& 0 & \cdots & 0 \\ S_2(q_2\cdot k_1) & S_2(q_2 \cdot k_2) & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ S_L(q_L\cdot k_1) & S_L(q_L \cdot k_2) & \cdots & S_L(q_L \cdot k_L) \\ \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_L \end{bmatrix} = \begin{bmatrix} S_1(q_1\cdot k_1)\cdot v_1 \\ S_2(q_2\cdot k_1)\cdot v_1 + S_2(q_2 \cdot k_2)\cdot v_2 \\ \vdots \\ S_L(q_L\cdot k_1)\cdot v_1 + S_L(q_L \cdot k_2)\cdot v_2 + \cdots + S_L(q_L \cdot k_L)\cdot v_L \\ \end{bmatrix}\]2-2 LLMs Inference: an Autoregressive Manner
Autoregressive inference is a common approach in large language models (LLMs), where the model generates one token at a time, conditioned on the previously generated tokens. Given an input sequence $x = [x_1, x_2, \ldots, x_t]$, the model predicts the probability of the next token $x_{t+1}$ by:
\[P(x_{t+1}|x_1, x_2, \ldots, x_t)\]This process continues recursively, producing coherent text output. For example, if a LLM tries to output a sentence "There is too much snow in winter", the model is firstly given the embedding of ["There"] and generate the next token “is”. Then, the input becomes ["There", "is"], and the model generates the next token "too"… When generating the token "winder", we will take ["There", "is", "too", "much", "snow", "in"] as input, and at this step the calculation within the attention module becomes
At next step, when we want to generate the content after "There is too much snow in winter", we need to take the tokens ["There", "is", "too", "much", "snow", "in", "winter"] as input, the computation within the above attention modulation becomes
Please note, at each inference step, we usually adopt the logits (i.e., output by the Language Modelling Head) related to the last token in the current sequence for next token prediction. In other words, only the hidden states in red color will participate the generation for the next token. Now, we can answer the following two questions:
-
Why we can accelerate the inference by caching $K,V$?
You may have observed that, from the generation of the tokens after
"in"($\textcolor{blue}{\text{blue}}$) and after"winter"($\textcolor{red}{\text{red}}$), $K$ and $V$ values from all the previous input tokens (i.e., $k_1,k_2,\cdots,k_L$ and $v_1, v_2, \cdots, v_L$) need to be reused, and $k_{L+1}, v_{L+1}$ for the new input token"winter"will be computed. Thus, after finishing a certain inference step, we can store the obtained $k$ and $v$ for the future reuse. That’s the mechanism behind KV-caching. Specifically, the longer the generated sequence is, more obvious the acceleration effect is. -
Why we don’t need to cache $Q$?
Obviously, at each inference step, only the $q_{t}$ for the current step is needed. We don’t need to store $q_{t}$ for future reuse.
3 KV-cache Implementation in GPT-2 Small
In this part, we will give a minimum implementation of GPT-2 small with KV-cache. We will compare the inference speed differences between with v.s. without KV-cache.
3-1 Introduction to GPT-2 series
OpenAI released the GPT-2 series in 2019 as a set of transformer-based language models designed for natural language generation. GPT-2 builds upon the foundation laid by GPT-1, with several architectural improvements:
- Decoder-Only Design: Like GPT-1, GPT-2 employs a transformer decoder architecture with masked self-attention, which prevents the model from attending to future tokens during training, ensuring causal language modeling.
- Larger Model Sizes: GPT-2 offers a range of model sizes from 124M to 1.5B parameters, compared to GPT-1’s 117M, allowing for more expressive language modeling.
-
Tied Embeddings: GPT-2 uses tied input and output embeddings, reducing the model’s memory footprint while improving performance. In other words, the weight matrix for the Language Modeling Head is the transpose of the weight matrix in the Token Embedding layer..
- Longer Context Window Size: GPT-2’s context window increased to 1024 tokens, supporting longer dependencies compared to GPT-1 (i.e., 512).
3-2 GPT-2 Model Architecture Comparison
The models come in four sizes: Small (124M), Medium (355M), Large (774M), and XL (1.5B). GPT-2 Small, with 124 million parameters, strikes a balance between model capacity and computational feasibility for real-time text generation.
| Model Size | Number of Parameters | Number of Layers | Number of Attention Heads | Hidden Size | Context Window Size |
|---|---|---|---|---|---|
| GPT-2 Small | 124M | 12 | 12 | 768 | 1024 |
| GPT-2 Medium | 355M | 24 | 16 | 1024 | 1024 |
| GPT-2 Large | 774M | 36 | 20 | 1280 | 1024 |
| GPT-2 XL | 1.5B | 48 | 25 | 1600 | 1024 |
In the following part, we adopted GPT-2 small as the implemented model and investigate the affect of KV-cache on the inference speed. The json configuration of GPT-2 small can be found in this link, which is also shown as follows:
{
"activation_function": "gelu_new",
"architectures": [
"GPT2LMHeadModel"
],
"attn_pdrop": 0.1,
"bos_token_id": 50256,
"embd_pdrop": 0.1,
"eos_token_id": 50256,
"initializer_range": 0.02,
"layer_norm_epsilon": 1e-05,
"model_type": "gpt2",
"n_ctx": 1024,
"n_embd": 768,
"n_head": 12,
"n_layer": 12,
"n_positions": 1024,
"resid_pdrop": 0.1,
"summary_activation": null,
"summary_first_dropout": 0.1,
"summary_proj_to_labels": true,
"summary_type": "cls_index",
"summary_use_proj": true,
"task_specific_params": {
"text-generation": {
"do_sample": true,
"max_length": 50
}
},
"vocab_size": 50257
}
Some core hyperparameters we need to use to define the model are:
"attn_pdrop": 0.1,
"embd_pdrop": 0.1,
"layer_norm_epsilon": 1e-05,
"n_ctx": 1024,
"n_embd": 768,
"n_head": 12,
"n_layer": 12,
"n_positions": 1024,
"vocab_size": 50257
3-3 A minimum implementation of GPT-2 Small
3-3-1 KV-cache Implementation in the Attention Module
The core is how to introduce KV-cache within the attention modules. Compare to a normal attention forward procese, we introduced the glag use_cache=False/True, and the tuple kv_past=None/(k_past, v_past) as the extra arguments. We firstly compute the $Q,K,V$ in the attention module, then we add the stored k_past, v_past to the new obtained key, value (for the token output from last round), and they will participate the attention operations. We also pass all the existing keys and values to kv_present and return it after the forward propagation.
If we adopt KV-cache, we first
class MultiHeadCausalAttention(nn.Module):
def __init__(self, config):
super(MultiHeadCausalAttention, self).__init__()
self.n_heads = config.n_head
self.n_embd = config.n_embd
self.n_positions = config.n_positions
assert self.n_embd % self.n_heads == 0
self.head_dim = self.n_embd // self.n_heads
self.c_attn = nn.Linear(self.n_embd, self.n_embd * 3)
self.c_proj = nn.Linear(self.n_embd, self.n_embd)
self.attn_dropout = nn.Dropout(config.attn_pdrop)
self.resid_dropout = nn.Dropout(config.resid_pdrop)
self.is_causal = True
def forward(self, hidden_states, use_cache=True, kv_past=None):
B, L, D = hidden_states.shape
qkv = self.c_attn(hidden_states).view(B, L, 3, self.n_heads, self.head_dim)
queries, keys, values = torch.unbind(qkv, dim=2) # 3*(B,L,h,D/h)
queries = queries.permute(0, 2, 1, 3) # (B,h,L,D/h)
keys = keys.permute(0, 2, 1, 3) # (B,h,L,D/h)
values = values.permute(0, 2, 1, 3) # (B,h,L,D/h)
##################################################################
if kv_past is not None:
k_past, v_past = kv_past
keys = torch.cat([k_past, keys], dim=-2)
values = torch.cat([v_past, values], dim=-2)
if use_cache:
kv_present = keys, values
else:
kv_present = None
##################################################################
attn_weights = (
torch.matmul(queries, keys.transpose(-1, -2)) / values.size(-1) ** 0.5
)
# create the mask
q_len, k_len = queries.size(-2), keys.size(-2)
causal_mask = torch.tril(
torch.ones((self.n_positions, self.n_positions), dtype=torch.bool)
).view(1, 1, self.n_positions, self.n_positions)
causal_mask = causal_mask[
:, :, k_len - q_len : k_len, :k_len
] # shape=(1,1,q_len, kv_len)
mask_value = torch.finfo(attn_weights.dtype).min
mask_value = torch.tensor(mask_value, dtype=attn_weights.dtype).to(
attn_weights.device
)
attn_weights = torch.where(causal_mask, attn_weights, mask_value) # (B,h,L,L)
attn_weights = F.softmax(attn_weights, dim=-1)
attn_weights = self.attn_dropout(attn_weights)
attn_out = torch.matmul(attn_weights, values) # (B,h,L,D/h)
attn_out = attn_out.permute(0, 2, 1, 3).reshape(B, L, D).contiguous()
attn_out = self.c_proj(attn_out)
attn_out = self.resid_dropout(attn_out)
return attn_out, kv_present
3-3-2 Complete the Whole Model
Then, we can complete a GPT-2 model with KV-cache with a slight modification. Please note we need to check if the length of the past tokens is zero (for use_cache=False) or equals to the number of restored keys/values (for use_cache=True).
import math
import json
from easydict import EasyDict as edict
import torch
import torch.nn as nn
def gelu_new(input):
return (
0.5
* input
* (
1.0
+ torch.tanh(
math.sqrt(2.0 / math.pi) * (input + 0.044715 * torch.pow(input, 3.0))
)
)
)
class FeedForward(nn.Module):
def __init__(self, config):
super(FeedForward, self).__init__()
n_embd = config.n_embd
self.c_fc = nn.Linear(n_embd, 4 * n_embd)
self.c_proj = nn.Linear(4 * n_embd, n_embd)
self.act = gelu_new
self.dropout = nn.Dropout(config.resid_pdrop)
def forward(self, hidden_states) -> torch.FloatTensor:
hidden_states = self.c_fc(hidden_states)
hidden_states = self.act(hidden_states)
hidden_states = self.c_proj(hidden_states)
hidden_states = self.dropout(hidden_states)
return hidden_states
## add the same arguments
class DecoderBlock(nn.Module):
def __init__(self, config):
super(DecoderBlock, self).__init__()
self.ln_1 = nn.LayerNorm(config.n_embd, eps=config.layer_norm_epsilon)
self.attn = MultiHeadCausalAttention(config)
self.ln_2 = nn.LayerNorm(config.n_embd, eps=config.layer_norm_epsilon)
self.mlp = FeedForward(config)
def forward(self, hidden_states, use_cache=True, kv_past=None):
residual = hidden_states
hidden_states = self.ln_1(hidden_states)
attn_out, kv_present = self.attn(
hidden_states, use_cache=use_cache, kv_past=kv_past
)
hidden_states = attn_out + residual
residual = hidden_states
hidden_states = self.ln_2(hidden_states)
ff_out = self.mlp(hidden_states)
hidden_states = residual + ff_out
return hidden_states, kv_present
class GPT2Model(nn.Module):
def __init__(self, config):
super(GPT2Model, self).__init__()
self.n_layer = config.n_layer
self.n_embd = config.n_embd
self.wte = nn.Embedding(config.vocab_size, self.n_embd)
self.wpe = nn.Embedding(config.n_positions, self.n_embd)
self.drop = nn.Dropout(config.embd_pdrop)
self.h = nn.ModuleList([DecoderBlock(config) for _ in range(config.n_layer)])
self.ln_f = nn.LayerNorm(self.n_embd, eps=config.layer_norm_epsilon)
self.lm_head = nn.Linear(config.n_embd, config.vocab_size, bias=False)
def forward(self, inputs_ids, position_ids, use_cache=True, kv_cache=None):
input_shape = inputs_ids.size()
##################################################################
if kv_cache is None:
past_length = 0
kv_cache = tuple([None] * len(self.h))
else:
past_length = kv_cache[0][0].size(-2)
##################################################################
if position_ids is None:
position_ids = torch.arange(
past_length,
input_shape[-1] + past_length,
dtype=torch.long,
device=inputs_ids.device,
)
position_ids = position_ids.unsqueeze(0)
inputs_embeds = self.wte(inputs_ids)
position_embeds = self.wpe(position_ids)
hidden_states = inputs_embeds + position_embeds
hidden_states = self.drop(hidden_states)
kv_present = [] if use_cache else None
for i in range(len(self.h)):
block, kv_past = self.h[i], kv_cache[i]
hidden_states, present_i = block(
hidden_states, use_cache=use_cache, kv_past=kv_past
)
##################################################################
if use_cache:
kv_present.append(present_i)
##################################################################
hidden_states = self.ln_f(hidden_states)
logits = self.lm_head(hidden_states)
return logits, kv_present
def model_inference(
model, input_ids, max_length=1000, use_cache=True, top_k=50, top_p=0.95
):
time_stamps = []
output_ids = input_ids
kv_cache = None if use_cache else []
print(tokenizer.decode(input_ids[0]), end="", flush=True)
model.eval()
with torch.no_grad():
for step in range(max_length):
t_s = time.time()
if use_cache:
# Use only the last token for efficient generation
position_ids = torch.tensor([[output_ids.size(-1)]])
logits, kv_cache = model(
output_ids[:, -1:],
position_ids,
use_cache=True,
kv_cache=kv_cache,
)
else:
# Use all tokens without KV cache
position_ids = torch.arange(output_ids.size(-1)).unsqueeze(0)
logits, _ = model(output_ids, position_ids, use_cache=False)
time_stamps.append(time.time() - t_s)
logits = logits[:, -1, :]
# Top-k and top-p sampling
logits = logits / 0.7 # Temperature scaling (1.0 = no scaling)
logits = logits + 1e-8 # Avoid NaNs by adding small epsilon
sorted_logits, sorted_indices = torch.sort(logits, descending=True)
cumulative_probs = torch.cumsum(F.softmax(sorted_logits, dim=-1), dim=-1)
sorted_indices_to_remove = cumulative_probs > top_p
if top_k > 0:
indices_to_remove = sorted_logits < sorted_logits[:, top_k - 1 : top_k]
sorted_indices_to_remove = sorted_indices_to_remove | indices_to_remove
sorted_logits[sorted_indices_to_remove] = -float("Inf")
probs = F.softmax(sorted_logits, dim=-1)
probs[torch.isnan(probs)] = 0 # Replace NaNs with zeros
probs[probs < 0] = 0 # Replace negative values with zeros
if torch.sum(probs) == 0:
# print("Warning: Sum of probabilities is zero. Falling back to uniform sampling.")
next_token_id = torch.randint(
0, logits.size(-1), (1, 1)
) # Fallback random token
else:
probs = probs / torch.sum(probs) # Re-normalize the distribution
next_token_id = torch.multinomial(probs, num_samples=1)
next_token_id = torch.gather(sorted_indices, -1, next_token_id)
output_ids = torch.cat([output_ids, next_token_id], dim=-1)
# Print generated token incrementally
print(tokenizer.decode(next_token_id[0]), end="", flush=True)
# Stop if EOS token is generated
if next_token_id.item() == tokenizer.eos_token_id:
break
return time_stamps
Please note that the inference input is different under these two modes (in function model_inference(...)):
- if
use_cache=False, we need to input all the current tokens;logits, _ = model(output_ids, position_ids, use_cache=False) - if
use_cache=True, we only need to input the last generated token, and also the cached keys and values for all previous tokens;logits, kv_cache = model(output_ids[:, -1:], position_ids, use_cache=True, kv_cache=kv_cache)
3-3-3 Check Inference Time
We compare the inference time with GPT-2 small, by randomly generating 500 tokens. The average inference time is shown below.
if __name__ == "__main__":
model_name = "gpt2"
with open("{}-config.json".format(model_name), "r") as f:
config = json.load(f)
config = edict(config)
model = GPT2Model(config=config)
w_dict = {}
# model weights availble at: https://huggingface.co/openai-community/gpt2/resolve/main/model.safetensors
with safetensors.safe_open("{}.safetensors".format(model_name), framework="pt") as f:
for k in f.keys():
w_dict[k] = f.get_tensor(k)
# GPT-2 use Conv1D, who works same as nn.Linear but with transposed weights
if k.startswith("h."):
w_dict[k] = w_dict[k].T
w_dict["lm_head.weight"] = w_dict["wte.weight"]
# gpt2.load_state_dict(w_dict)
model.load_state_dict(w_dict, strict=False)
tokenizer = AutoTokenizer.from_pretrained(model_name)
# Input prompt
prompt = "Once upon a time in a distant kingdom, there was a wise old king who"
inputs = tokenizer(prompt, return_tensors="pt")
input_ids = inputs["input_ids"]
# Generate a long sequence with kv-cache
max_length = 1000
output_ids = input_ids
kv_cache = None
time_stamps = model_inference(
model, input_ids, max_length=500, use_cache=False, top_k=30, top_p=0.9
)
print("\naverage time: {:.2f}s/token".format(np.mean(time_stamps)))
# average time: 0.13s/token
time_stamps = model_inference(
model, input_ids, max_length=500, use_cache=True, top_k=30, top_p=0.9
)
print("\naverage time: {:.2f}s/token".format(np.mean(time_stamps)))
# average time: 0.03s/token
The inference time change along the generation process is visualized in the following picture. We can observe that, if without KV-cache, the inference time will dramatically increase in the later steps; while the KV-cache strategy can make the inference time at quasi-constant level.
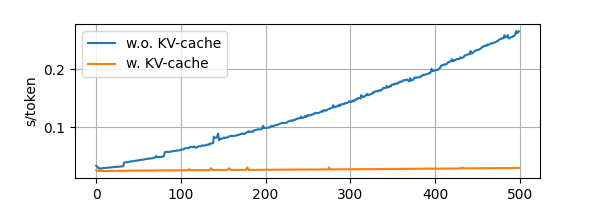
4 No Free Lunch: Space for Time
Please note that KV-cache reduced the inference time by storing some reusable keys and values within the attention module. THus, the cost will be the extract space to store these K and V. A longer sequence is generated, the more space will be needed.
Enjoy Reading This Article?
Here are some more articles you might like to read next: